THE EQUIVALENCE OF HEAT AND WORK

§ 1. NatuTe of Heat

Until recently it was the generally accepted view that Beat was a special substance, which was present in bodies in greater or less quantity, and which produced thereby their higher or lower temperature; which was also sent forth from bodies, and in that case passed with immense speed through empty space and through such cavities as ponderable bodies contain, in the form of what is called radiant heat. In later days has arisen the other view that Heat is in reality a mode of motion. According to this view, the heat found in bodies and determining their temperature is treated as being a motion of their ponderable atoms, in which motion the ether existing within the bodies may also participate; and radiant heat is looked upon as an undulatory motion propagated in that ether.

It is not proposed here to set forth the facts, experiments, and inferences, through which men have been brought to this altered view on the subject; this would entail a reference here to much which may be better described in its own place during the course of the book. The conformity with experience of the results deduced from this new theory will probably serve better than anything else to establish the foundations of the theory itself.

We will therefore start with the assumption that Heat consists in a motion of the ultimate particles of bodies and of ether, and that the quantity of heat is a measure of the Vis Viva of this motion. The nature of this motion we shall not attempt to determine, but shall merely apply to Heat the ptinciple of the equivalence of Vis Viva and Work,which applies to motion of every kind; and thus est~blish a principle which may be called the first main Principle of the M.echanical Theory of Heat.

§ 2. Positive and negative values of Mechanical Work

In § 1 of the Introduction the mechanical work done in the movement of a point under the action of a force was defined to be The product of the distance moved through and of the component of the force resolved in the direction of motion. The work is thus positive if the component of force in the line of motion lies on the same side of the initial point as the element of motion, and negative if it falls on the opposite side. From this definition of the positive sign of mechanical work follows the . principle of the equivalence of Vis Viva and Work, viz. The increase in the Vis' Viva is equal to the work done, or equal to the increase in total work.

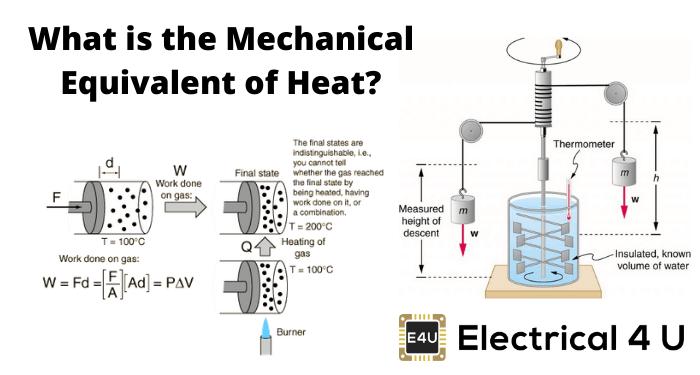
The question may also be looked at from another point of view. If a material point has once .been set in motion, it can continue. this movement, on account of its momentum, even if the force acting on it tends in a direction opposite to that of the motion; though its velocity, and therewith its Vis Viva, will of course be diminishing all the time. A material point acted on by gravity for tlxample, if it has received an upward impulse, can continue to move against the force of gravity, although the latter is continually diminishing the velocity given by the impulse. In such a case the work, if considered as work done by the force, is negative. Conversely however we may reckon work as· positive in cases where a force is overcome by the momentum of a previously acquired motion, as negative in cases where the point follows the direction of the force. Applying the form of expression introduced in § 1 of the Introduction, in which the distinction between the two opposite directions of the component of force is indicated by different words, we may express the foregoing more simply as follows: we may determine that not the work done, but the work destroyed, by a force shall be reckoned as positive. On this method of denoting work done, the principle of the equivalence of Vis Viva and Work takes the following form: The decrease t'n the Vis Viva is equal to the increase in the Work done, or The sum of the Vis Viva'arrd Work done is constant. This latter form will be found very convenient in what follows.

In the case of such forces as have an Ergal, the meaning' of that quantity was defined (in § 6 of the Introduction) ill such a manner that we must say, 'The Work done is equal

to the decrease in the Ergal.' If we use the method of denoting work just described, we must say on the contrary, 'The work done is equal to the increase in the Ergal;' and if the constant occurring as one term of the Ergal be determined in a particular way, we may then regard the Ergal as simply an expression for the work done.

§ 3. Expression for the first Fundamental Principle

Having fixed as above what is to be the positive sign for work done, we may now I!tate as follows the first main Principle of the Mechanical Theory of Heat.

In all cases where work is produced by heat, a quantity of heat is consumed proportional to the work done; and inversel:/, by the e.xpenditure of the same amOltnt of work the sume quantity of heat may be produced.

This follows, on the mechanical conception of heat, from the equivalence of Vis Viva and Work, and is named The Principle of the Equivalence of Heat and Work. .

If heat is consumed, aud work thereby produced, we may say that heat has transformed itself into work; and conversely, if work is expended and heat thereby produced, we may say that work has transformed itself into heat. Using this mode of expression, the foregoing principle takes the

following form : Work may transform itself into heat, and heat conversely into work, the quantity of the one bearing alway.s a fixed proportion to that of the other.

This principle is established by means of many phenomena which have been long recognized, and of late years has been confirmed by so many experiments of different kinds, that we may accept it, apart from the circumstance of its forming a special case of the general mechanical principle of the Conservation of Energy, as being a principle directly derived from experience and observation.